ArrayList vs LinkedList
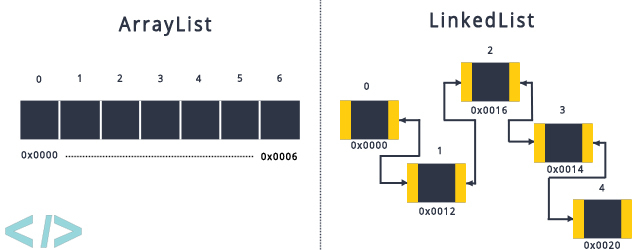
ArrayList는 내부적으로 배열로 구현되어 있으며, 배열의 크기를 동적으로 조절할 수 있다.
ArrayList는 인덱스를 이용한 요소 접근이 매우 빠르기 때문에, 특정 요소를 검색하는 작업에 유용한다.
또한 ArrayList는 LinkedList에 비해 메모리 사용량이 적다.
그러나 ArrayList는 요소의 삽입과 삭제 작업 시 배열 내에서 해당 요소 이후의 요소들을 전부 이동시켜야 하기 때문에, 요소의 삽입과 삭제가 빈번하게 일어나는 경우에는 성능이 저하될 수 있습니다.
LinkedList는 이중 연결 리스트로 구현되어 있으며, 각 요소는 자신의 이전 요소와 다음 요소를 가리키는 두 개의 포인터를 가지고 있다.
따라서 LinkedList는 요소의 삽입과 삭제가 빈번하게 일어나는 상황에서 유용하다.
예를 들어, 리스트의 중간에 새로운 요소를 삽입하는 경우, 해당 요소의 위치를 찾아내기만 하면 삽입 작업이 매우 빠르다.
그러나 LinkedList는 인덱스를 이용한 요소 접근이 느리기 때문에, 특정 요소를 빠르게 검색하는 작업에는 적합하지 않습니다.
1. 데이터의 검색/삽입/삭제 시 성능 비교
1.1 데이터 검색
ArrayList는 인덱스를 활용하기 때문에 데이터에 빠른 접근이 가능하다. -> O(1)
반면 LinkedList는 데이터를 찾을 때마다 첫 번째 데이터부터 차례대로 접근해야 하기 때문에 시간이 많이 걸린다. -> O(n)
1.2 데이터 삽입
ArrayList는 데이터를 추가할 때마다 내부 배열의 크기를 체크하고, 크기가 부족하다면 새로운 배열을 할당하여 복사하는 작업을 수행합니다. 이 작업은 무거운 작업이기 때문에 삽입 속도가 느리다. -> O(n)
LinkedList는 새로운 노드를 삽입할 때 해당하는 노드의 포인터 값만 수정하면 된다. 따라서 LinkedList는 삽입 위치가 불분명하거나 중간 삽입이 빈번히 일어나는 경우에 유용하다. -> Search Time + O(1)
하지만 리스트의 맨 끝에 데이터를 추가하는 경우에는 삽입 위치를 찾을 필요가 없기 때문에, LinkedList보다 ArrayList가 더 빠르게 작동할 수 있다.
1.3 데이터 삭제
ArrayList는 데이터를 삭제할 때 해당 인덱스를 삭제하고, 뒤에 있는 모든 요소들을 앞으로 이동시켜야 한다. 이 작업은 매우 무거운 작업이기에 삭제 속도가 느리다. -> O(n)
LinkedList는 데이터를 삭제할 때 삭제할 노드의 위치를 찾아서 해당 노드의 이전 노드와 다음 노드를 연결하면 된다. 따라서 LinkedList는 중간 삽입이 빈번한 경우나 삭제 위치가 불분명한 경우에 유용하다. -> Search Time + O(1)
그러나 삭제 위치가 맨 끝에 위치한 경우에는 LinkedList보다 ArrayList가 더 빠르게 작동할 수 있다.
결론적으로 데이터의 검색이 잦은 경우 ArrayList가 적합하고, 데이터의 삽입 및 삭제가 잦은 경우 LinkedList가 적합하다.
2. Array 기반으로 LinkedList 구현
public class Node { // LinkedList의 노드
private Node prev;
private Node next;
private double data;
public Node(double data) {
this.data = data;
}
public Node getPrev() {
return prev;
}
public void setPrev(Node prev) {
this.prev = prev;
}
public Node getNext() {
return next;
}
public void setNext(Node next) {
this.next = next;
}
public double getData() {
return data;
}
public void setData(double data) {
this.data = data;
}
}
public class DoubleLinkedList { // Array를 사용한 이중 연결 리스트
private Node[] nodes; // 노드들을 담을 Array 선언
private int size; // 현재 연결되어 있는 노드 수
private int capacity; // LinkedList의 크기
public DoubleLinkedList(int capacity) { // 생성자
this.nodes = new Node[capacity];
this.size = 0;
this.capacity = capacity;
}
public void add(double data) { // 데이터 삽입
if (this.size == this.capacity) { // 리스트가 꽉 참
throw new ArrayIndexOutOfBoundsException();
}
Node node = new Node(data);
if (this.size == 0) { // 첫 번째 노드가 삽입된 것이므로 포인터가 연결될 필요가 없음
this.nodes[0] = node;
} else { // 이전의 노드의 다음 노드로 현재 삽입된 노드를 연결시키고, 현재 삽입한 노드와 이전 노드를 연결
this.nodes[this.size] = node;
this.nodes[this.size - 1].setNext(node);
node.setPrev(this.nodes[this.size - 1]);
}
this.size++; // size 증가
}
public void remove(int index) { // 데이터 삭제
if (index < 0 || index >= this.size) { // 유효하지 않은 index
throw new IndexOutOfBoundsException();
}
if (index == 0) { // 제일 첫 노드를 제거
this.nodes[1].setPrev(null);
} else if (index == this.size - 1) { // 제일 마지막 노드를 제거
this.nodes[index - 1].setNext(null);
} else { // 중간에 위치한 노드를 제거
this.nodes[index - 1].setNext(this.nodes[index + 1]);
this.nodes[index + 1].setPrev(this.nodes[index - 1]);
}
for (int i = index; i < this.size - 1; i++) { // 제거 후 한 칸씩 앞으로 당기기
this.nodes[i] = this.nodes[i + 1];
}
this.nodes[this.size - 1] = null; // 제일 마지막 노드는 비어야 함
this.size--; // size 감소
}
public double get(int index) { // 노드의 데이터 조회
if (index < 0 || index >= this.size) { // 유효하지 않은 index
throw new IndexOutOfBoundsException();
}
return this.nodes[index].getData();
}
}3. ArrayList 기반으로 LinkedList 구현
위의 Array를 기반으로 구현한 것과 차이는 Array는 크기가 정적으로 정해져있기 때문에 최대 크기를 벗어나서 데이터를 삽입하려고 하면, Exception을 발생시켰지만 ArrayList를 사용한 방식에서는 동적으로 크기가 변경될 수 있기 때문에 Exception이 발생하지 않는다.
public class Node { // LinkedList의 노드
private Node prev;
private Node next;
private double data;
public Node(double data) {
this.data = data;
}
public Node getPrev() {
return prev;
}
public void setPrev(Node prev) {
this.prev = prev;
}
public Node getNext() {
return next;
}
public void setNext(Node next) {
this.next = next;
}
public double getData() {
return data;
}
public void setData(double data) {
this.data = data;
}
}
public class DoubleLinkedList { // ArrayList를 사용한 이중 연결리스트
private ArrayList<Node> nodes; // 노드들을 담을 ArrayList 선언
public DoubleLinkedList() { // 생성자
this.nodes = new ArrayList<>();
}
public void add(double data) { // 데이터 삽입
Node node = new Node(data);
if (this.nodes.size() == 0) { // 첫 번째 데이터 삽입
this.nodes.add(node);
} else {
Node lastNode = this.nodes.get(this.nodes.size() - 1);
lastNode.setNext(node);
node.setPrev(lastNode);
this.nodes.add(node);
}
}
public void remove(int index) { // 데이터 제거
if (index < 0 || index >= this.nodes.size()) { // 유효하지 않은 index
throw new IndexOutOfBoundsException();
}
Node nodeToRemove = this.nodes.get(index); // 제거할 노드가
if (nodeToRemove.getPrev() != null) { // 가장 앞의 노드가 아니라면
nodeToRemove.getPrev().setNext(nodeToRemove.getNext()); // 제거할 노드의 이전 노드와 다음 노드를 연결
}
if (nodeToRemove.getNext() != null) { // 가장 마지막 노드가 아니라면
nodeToRemove.getNext().setPrev(nodeToRemove.getPrev()); // 제거할 노드의 다음 노드와 이전 노드를 연결
}
this.nodes.remove(index); // 제거
}
public double get(int index) { // 노드의 데이터 조회
if (index < 0 || index >= this.nodes.size()) { // 유효하지 않은 index
throw new IndexOutOfBoundsException();
}
return this.nodes.get(index).getData();
}
}스택, 큐
1. 스택

먼저 스택은 한 쪽 끝에서만 자료를 넣고 빼는 작업이 이루어지는 자료구조이다.
LIFO (Last In First Out) 방식으로 동작하며 가장 최근에 스택에 삽입된 자료의 위치를 top이라 한다.
스택의 맨 위 요소, 즉 top에만 접근이 가능하기에 top이 아닌 위치의 데이터에 대한 접근, 삽입, 삭제는 모두 불가능하다.
다음과 같은 상황에서 스택을 사용할 수 있다.
- 재귀 알고리즘
- DFS 알고리즘
- 작업 실행 취소와 같은 역추적 작업이 필요할 때
- 괄호 검사, 후위 연산법, 문자열 역순 출력 등
다음은 스택을 구현한 것이다.
public class Stack {
private int top;
private int capacity;
private int[] elements;
public Stack(int capacity) { // 생성자
this.top = -1;
this.capacity = capacity;
this.elements = new int[capacity];
}
public boolean isEmpty() { // stack이 비었는지 확인
return this.top == -1; // top이 -1이면 아무런 데이터도 없다는 뜻
}
public boolean isFull() { // stack이 꽉 찼는지 확인
return this.top == this.capacity - 1; // top이 최대 크기와 같은지
}
public void push(int element) { // stack에 데이터 삽입
if (isFull()) { // stack이 꽉 찼으면 데이터 삽입 불가
throw new IllegalStateException("Stack is full");
}
this.elements[++this.top] = element;
}
public int pop() { // stack에서 데이터 삭제
if (isEmpty()) { // stack이 비었으면 데이터 삭제 불가
throw new NoSuchElementException("Stack is empty");
}
return this.elements[this.top--];
}
public int peek() { // stack의 top에 존재하는 데이터를 조회
if (isEmpty()) { // stack이 비었으면 데이터 조회 불가
throw new NoSuchElementException("Stack is empty");
}
return this.elements[this.top];
}
}2. 큐

한쪽에서만 데이터의 삽입과 삭제가 이루어지는 스택과 달리 큐는 한 쪽 끝에서는 데이터의 삽입이 다른 한 쪽 끝에서는 삭제가 이루어진다.
FIFO (First In First Out) 으로 동작하며 데이터가 삽입되는 곳을 rear, 데이터가 제거되는 곳을 front라 한다.
큐 역시 스택과 마찬가지로 중간에 위치한 데이터에 대한 접근이 불가능하다.
다음과 같은 상황에서 큐를 사용할 수 있다.
- 데이터를 입력된 순서대로 처리해야 할 때
- BFS 알고리즘
- 프로세스 관리
- 대기 순서 관리
다음은 큐를 구현한 것이다.
public class Queue {
private int front;
private int rear;
private int capacity;
private int[] elements;
public Queue(int capacity) { // 생성자
this.front = 0;
this.rear = -1;
this.capacity = capacity;
this.elements = new int[capacity];
}
public boolean isEmpty() { // queue가 비었는지 확인
return this.rear < this.front; // rear가 front보다 작다면 queue는 빈 상태
}
public boolean isFull() { // queue가 꽉 찼는지 확인
return this.rear == this.capacity - 1; // rear가 (전체 크기 - 1)과 같다면 queue는 꽉 찬 상태
}
public void enqueue(int element) { // queue에 데이터 삽입
if (isFull()) { // queue가 꽉 찼으면 데이터 삽입 불가
throw new IllegalStateException("Queue is full");
}
this.elements[++this.rear] = element;
}
public int dequeue() { // queue에서 데이터 제거
if (isEmpty()) { // queue가 비었으면 데이터 제거 불가
throw new NoSuchElementException("Queue is empty");
}
return this.elements[this.front++];
}
public int peek() { // queue의 front에 존재하는 데이터 조회
if (isEmpty()) { // queue가 비었으면 데이터 조회 불가
throw new NoSuchElementException("Queue is empty");
}
return this.elements[this.front];
}
}
3. 원형 큐

일반적인 선형 큐의 단점을 보완하기 위한 것으로 배열의 처음과 끝이 연결되어 있는 형태를 가지고 있다.
선형 큐에서 데이터를 꺼내올 때 배열의 가장 앞에 있는 데이터를 꺼내오기 때문에 front의 데이터를 제거한 후에 그 다음 인덱스의 데이터들을 한 칸씩 모두 이동해야 했었다.
즉, 자료 하나를 꺼낼 때마다 O(n)만큼의 시간 복잡도를 요구하므로 상당히 비효율적이다.
하지만 원형 큐에서는 데이터의 맨 앞과 맨 뒤 위치를 기억하기 때문에 선형 큐처럼 데이터를 삭제할 때마다 매번 한 칸씩 당겨오지 않아도 된다.
그림에서 볼 수 있듯이 공백 상태와 포화 상태를 구분하기 위해 하나의 공간을 비워두었으며, front == rear인 경우에 원형 큐는 Empty이고, front == (rear+1) % MAX_QUEUE_SIZE인 경우에는 포화 상태인 것이다.
다음은 원형 큐를 구현한 것이다.
public class CircularQueue {
private int front;
private int rear;
private int capacity;
private int[] elements;
public CircularQueue(int capacity) { // 생성자
this.front = 0;
this.rear = -1;
this.capacity = capacity;
this.elements = new int[capacity];
}
public boolean isEmpty() { // 원형 큐가 비었는지 확인
return this.rear == -1;
}
public boolean isFull() { // 원형 큐가 꽉 찼는지 확인
return ((this.rear + 1) % this.capacity) == this.front;
}
public void enqueue(int element) { // 원형 큐에 데이터 삽입
if (isFull()) { // 원형 큐가 꽉 찼다면 데이터 삽입 불가
throw new IllegalStateException("Queue is full");
}
// rear가 최대 index를 넘어가더라도 원형 큐이기 때문에 처음으로 돌아오도록 구현
this.rear = (this.rear + 1) % this.capacity;
this.elements[this.rear] = element;
if (this.front == -1) { // 원형 큐가 비고 난 후 처음으로 들어온 데이터
this.front = this.rear;
}
}
public int dequeue() { // 원형 큐에 데이터 삭제
if (isEmpty()) { // 원형 큐가 비었다면 데이터 삭제 불가
throw new NoSuchElementException("Queue is empty");
}
int element = this.elements[this.front];
if (this.front == this.rear) { // 마지막 남은 데이터를 삭제할 경우
this.front = -1;
this.rear = -1;
} else { // front가 최대 index를 넘어가더라도 원형 큐이기 때문에 처음으로 돌아오도록 구현
this.front = (this.front + 1) % this.capacity;
}
return element;
}
public int peek() { // front에 존재하는 데이터 조회
if (isEmpty()) { // 원형 큐가 비었다면 데이터 조회 불가
throw new NoSuchElementException("Queue is empty");
}
return this.elements[this.front];
}
}4. 덱
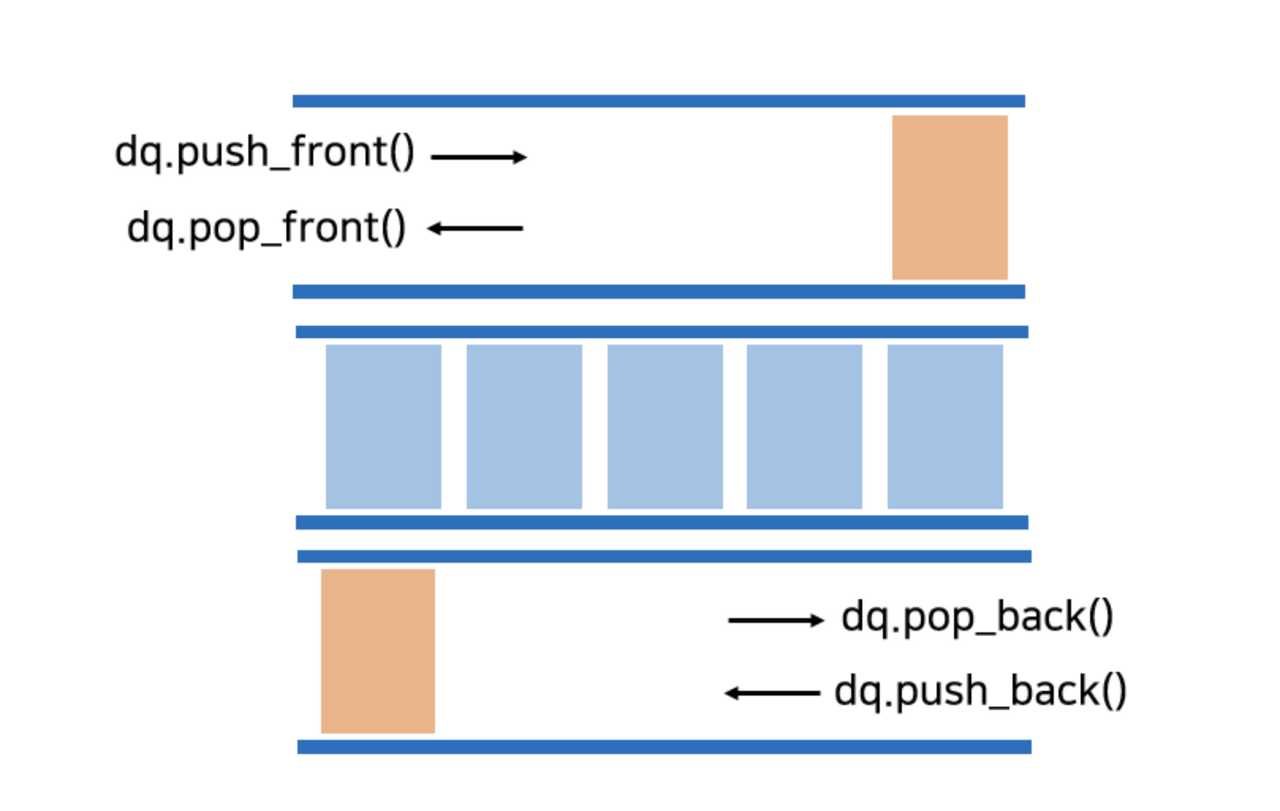
Deque(Double Ended Queue)는 한 쪽에서만 삽입, 다른 한쪽에서만 삭제가 가능했던 큐와 달리 front, rear 모두에서 삽입과 삭제가 가능한 큐이다.
Deque의 크기는 동적으로 변할 수 있기 때문에, 크기의 제한이 없다.
데이터의 삽입 삭제가 빠르고 앞뒤에서 삽입, 삭제가 모두 가능하다. 다만 스택과 큐에 비해 구현이 어렵다.
데이터를 앞, 뒤쪽에서 모두 삽입 또는 삭제하는 작업이 필요한 경우에 사용한다.
다음은 덱을 구현한 것이다.
public class ArrayDeque<E> {
private int front; // Deque의 맨 앞 요소 인덱스
private int rear; // Deque의 맨 뒤 요소 인덱스
private int capacity; // 배열의 크기
private E[] array; // Deque를 저장할 배열
public ArrayDeque(int capacity) {
this.front = 0;
this.rear = 0;
this.capacity = capacity;
this.array = (E[]) new Object[capacity];
}
// 덱이 비어있는지 확인
public boolean isEmpty() {
return front == rear;
}
// 덱이 꽉 차있는지 확인
public boolean isFull() {
return front == (rear + 1) % capacity;
}
// 덱의 크기 반환
public int size() {
if (front <= rear) {
return rear - front;
} else {
return capacity - front + rear;
}
}
// 덱의 맨 앞에 요소 추가
public void addFirst(E element) {
if (isFull()) {
throw new RuntimeException("Deque is full");
}
front = (front - 1 + capacity) % capacity;
array[front] = element;
}
// 덱의 맨 뒤에 요소 추가
public void addLast(E element) {
if (isFull()) {
throw new RuntimeException("Deque is full");
}
array[rear] = element;
rear = (rear + 1) % capacity;
}
// 덱의 맨 앞 요소 제거
public E removeFirst() {
if (isEmpty()) {
throw new RuntimeException("Deque is empty");
}
E element = array[front];
front = (front + 1) % capacity;
return element;
}
// 덱의 맨 뒤 요소 제거
public E removeLast() {
if (isEmpty()) {
throw new RuntimeException("Deque is empty");
}
rear = (rear - 1 + capacity) % capacity;
E element = array[rear];
return element;
}
// 덱의 맨 앞 요소 반환
public E peekFirst() {
if (isEmpty()) {
throw new RuntimeException("Deque is empty");
}
return array[front];
}
// 덱의 맨 뒤 요소 반환
public E peekLast() {
if (isEmpty()) {
throw new RuntimeException("Deque is empty");
}
int index = (rear - 1 + capacity) % capacity;
return array[index];
}
}출처
ArrayList, LinkedList 비교
velog.io
[자료구조] 스택 Stack, 큐 Queue, 덱 Deque
새로운 시리즈는 자료구조이다. 진즉좀 정리 해 둘걸,,, 다 아는 내용이어도 이렇게 정리하려고 하니 참 시간도 꽤 걸리고 더 깊게 공부해야 하기도 하고,,, 암튼 자료구조 시리즈의 첫번째 포스
velog.io
'개발 > CS' 카테고리의 다른 글
| (CS) 네트워크 기본 용어 정리 (0) | 2023.05.04 |
|---|---|
| (CS) 단일 연결 리스트 vs 원형 연결 리스트, Stack으로 Queue 구현, 원형 큐 구현 (0) | 2023.04.26 |
| (CS) 캐시 메모리, 메모리 관리 기법, 페이지 교체 알고리즘 (1) | 2023.03.27 |
| (CS) 데드락, 기아 상태, 스케줄링 (0) | 2023.03.22 |
| (CS) 프로세스, 스레드, 프로세스 동기화 기법 (0) | 2023.03.16 |
